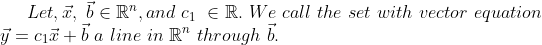Linear Algebra2: Linear Independence, Basis, and Spans

We talk about the concept of a linear combination, span & spanning sets, linear independence, basis, lines, planes, and hyperplanes. Very little programming for this one, but it's very math heavy.

Introduction

This will add in a lot of definitions to the vectors concept in part one. Make sure you go through the part 1 in great detail, and then grab some coffee for this one. There are many definitions covered in this one. A lot of these will come back once again, when we deal with concepts for a Machine Learning Engineer role, and when we deal with things like dimensionality reduction with the principal components analysis (eigenvalues and vectors).

Table of Contents:

1. Linear Combination

2. Span & Spanning Sets

3. Linear Independence

4. Basis

5. Line, Plane, & Hyperplanes

1 - Linear Combination

Concept

If a vector is equal to the sum of scalar multiple of several other vectors. We say that this vector is a linear combination of the other vectors. in the example below, we have a set of k vectors. Here is the mathematical interpretation of it below.

Example

Let’s say we have 2 vectors: [1,2], and [1,1]. Then the following are a linear combination of our 2 vectors:

2 - Span & Spanning Sets

Concept

If we have a set of vectors, lets call the set B. Then the span of B is defined as every single vector that is a linear combination of B. Now lets called this new set X. We then say that X is spanned by B, and that B is a spanning set of X.

Example

Let’s see if the vector [1,3] belongs to the span of the set {[2,-1],[3,3]}

So, the answer would be yes it does

3 - Linear Independence

Concept

In linear algebra, if we have a set of vectors, call this set S. Then if we can come up with a sum of scalar multiple using all of the vectors in there, so that we end up with a 0. Where there has to be at least 1 scalar in the multiple, that isn’t a 0, then we can say that the set S is considered to be linearly dependent.

If we cannot come up with the scalars to make it equal to 0, then we say that this set S is linearly independent. Here is the mathematical notation for it.

Basically, if the only way to get the scalar sum of the set of vectors to get 0 is to make every constant 0, then it is linearly independent. This is extremely important for concepts like dimensionality reduction, as if the set of vectors is linearly dependent, we can kick out one of the vectors, and still retain most of the information.

Example

Let’s see if the set S= {[7,-14,6],[-10,15,15/14],[-1,0,3]} is linearly independent. Or if it is linearly dependent.

4 - Basis

Concept

A set S of vectors in a vector space V is called a basis if every element of V can be written in a linear combination using vectors only in S. Here is the mathematical definition:

Example

Check if B={[1,0],[0,1]} is a basis for ​R^2

5 - Line, Plane, & Hyperplanes

Concept

From the diagram above, we can see that we can that a line is a solution of an equation in a 2D space. A simple plane is a solution in a 3D space, and a hyperplane is a solution to an equation in 3D or higher dimensional space. Here is the mathematical definition below, notice how similar for the line is, compared to the traditional equation of a line.

Line

Plane

Hyperplane

In Data Science, we will start off by creating simple lines of best fit (2D), and then very quickly take our solution and add several dimensions to it, and very quickly go from working with lines, to working with hyperplanes.