Matrices made super easy

Linear Algebra 4: You will spend about 90% of your DS career data wrangling, messing with data to make it into a usable format, so that you can eventually run models on it.

Required Readings

Make sure you understand how vectors work, and how to work with them in both R, and Python. Click here for details.

Table of Contents:

1. Recap of Vectors

2. Where do you use this?

3. How do you make a matrix?

4. Properties of Matrices

5. Summary

1 - Recap of Vectors

Vectors are basically a chunk of data that we have. It could be a simple set of numbers, or it could be a simple list of number (Python), or a vector or numbers (R). From a vector, we can do basic statistical analysis, such as the 5 number summary to get some information on how the distribution of numbers looks like in our vector.

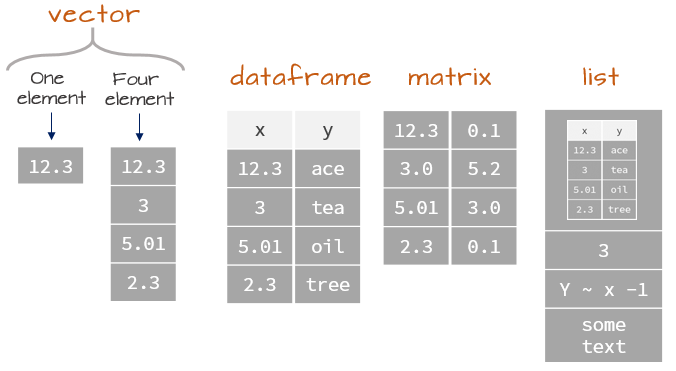
Now, what if instead of just looking at 1 vector, we were instead looking at a series of vectors at the same time? Introducing something called a matrix.

2 - Where do you use this?

Unless you are working with unstructured data (NLP & image/video recognition), 90% of you time will be spent looking at a table, which has several columns & rows. That dataset can be represented by a simple matrix. If you look at the above diagram, you can see that a matrix is basically like a simple table. Click here to do some data wrangling.

In other words, you will spend 90% of your time staring at a matrix/array of data. The model building aspect only takes about 10% of the time.

Here is another simple visual to help illustrate this. You can think of each dataframe as a simple dataset, and a matrix is the same thing, except without the labeling

3 - How do you make a matrix?

Mathematical

Here is the mathematical definition of a matrix. You can think of it as a simple table which has m number of rows, and n number of columns. Hence it has a total of m*n = mn entries.

For the sake of simplicity for this whole post, we will assume

R

The simplest way to create a matrix in R is to use c( ) in order to make a vector. Then, we can use rbind( ) in order to basically do a rowbind 2 times.

Here is the above A matrix being recreated in R.

Here is the output.

Python

in order to make a matrix in Python, we will rely on the numpy library and basically make ourselves a 2 dimensional (2D) array. Click here if you need help setting up libraries.

Here is the code in Python, alongside its output.

4 - Properties of Matrices

Matrix Addition/Subtraction

Mathematical

If we want to do matrix addition, then all we do is add up the ij-th element in matrix A with the ij-th element in matrix B for all of the elements in there.

Here is an example to help understand.

Note: Subtraction works the exact same way, except instead of adding the numbers you are subtracting them.

R

We already have the matrix A from our earlier example, now let’s construct matrix B.

We can add the matrices together by simply using the + sign, and here is everything put together.

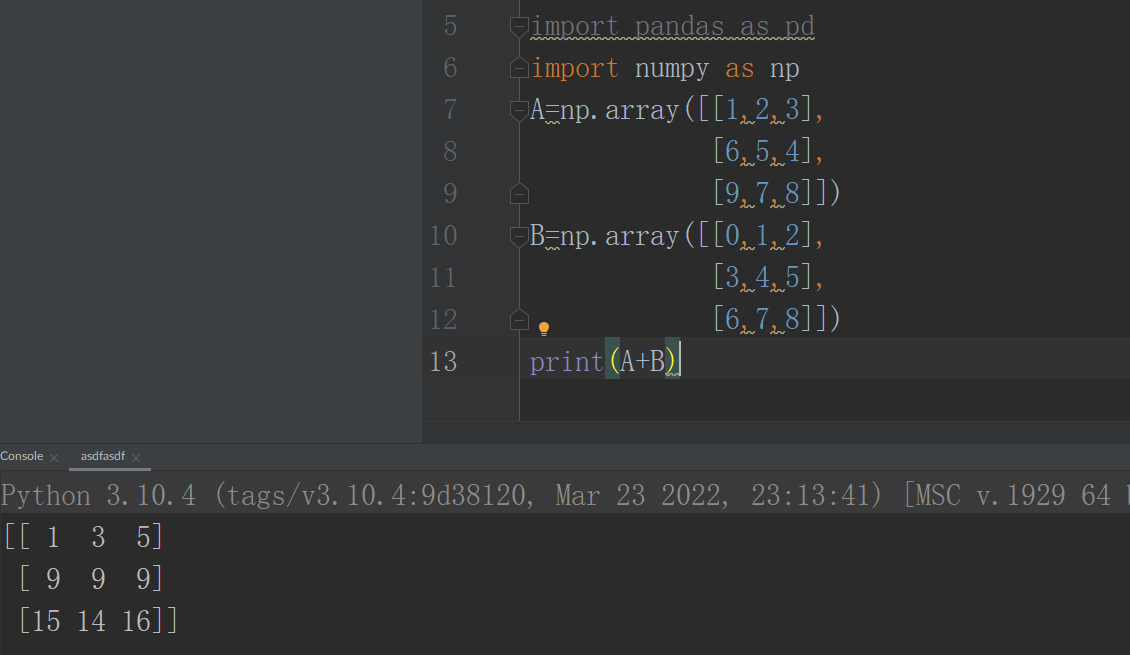
Python

Here is the code, with the output in Python:

Just like in R, we are using the + sign for the addition.

Matrix Transpose

Mathematical

One of the weird things we have with matrices is something called the transpose of a matrix. Basically what this thing does is just flip the rows and the columns. In other words, the entry that was located on row i, and column j is now located on row j, and column i. Here is the mathematical definition:

Here is an example, using our A matrix from up above.

R

If we want to transpose a matrix in R, we can just use the t( ) function. Here is how it looks like in practice

Python

If we want to transpose a matrix in Python, the numpy library offers us a transpose( ) function we can use on our arrays. Here is what it looks like:

Matrix Multiplication

Mathematical

If we have 2 matrices A & B. If we wanted to do AB, then in order to do this, we will basically have to Transpose B, and then multiply and add each vector in B with each horizontal vector in A. Here is the mathematical explanation for it:

It’s a bit difficult to understand just from the formula above, so let’s multiply our above A and B matrices together in a step by step manner.

R

In order to do matrix multiplication in R, we can just do %*%. Here it is below:

Python

In order to do matrix multiplication in Python, we can rely on the matmul( ) function from the numpy library:

5 - Summary

In general, you will be working with matrices quite often, the above is just a simple introduction to some of their basic properties, we will go more in depth with them soon. One thing you will have noticed is that R tends to have much smaller requirements for applying functions than Python, this is because R was built up as a statistical analysis language, whereas Python was meant as more of a general purpose one. You will see more examples of these little nuances when we get to some of the model building aspects.