Python Data Skills 8: Data Visualization

Histograms, QQ Plots, Box Plots, Violin Plots, Scatter Plots, Line Plots, HeatMaps

Not much to say here. There’s a lot, and most people only know 1 or 2 techniques below. Would recommend adding this page to your bookmarks as well. The visualizations are great for reports, or for showing to the higher ups.

Table of Contents

1. Histograms & QQ plots

2. Grouped Boxplots

3. Violin Plot

4. Scatter Plots

5. Line Plots

6. HeatMaps

1 - Histograms & QQ plots

A good first step is to understand the distribution of your data. Do this before delving into machine learning models or sophisticated data analysis. 2 powerful tools to aid this understanding are histograms and Quantile-Quantile (Q-Q) plots.

1.1 Their Role in Outlier Detection

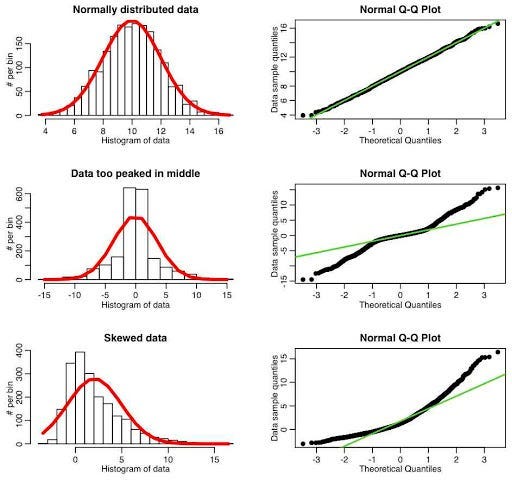
A histogram is a graphical representation of the frequency distribution of a dataset. It is an estimate of the probability distribution of a continuous variable. To construct a histogram, the first step is to "bin" the range of values. That is, divide the entire range of values into a series of intervals. Then count how many values fall into each interval. The plotted vertical bars show the frequency (the number of data points) that fall within each bin.

Histograms allow for a visual inspection of the data for its underlying distribution. (e.g., normal distribution), outliers, skewness, and kurtosis. Outliers will often appear as bars detached from the bulk of the data in a histogram.

Histogram

A stacked histogram allows the comparison of distributions between groups. Each bar in the histogram is divided into sub-bars. These sub-bars are corresponding to the group and the proportion of the group within the bin. This is particularly useful when the dataset consists of several different categories. It is also useful when you're interested in comparing these categories' distributions.

Stacked Histogram

1.2 Introduction to QQ Plots

A Q-Q (quantile-quantile) plot is a graphical tool. It's used to assess if a dataset follows a certain theoretical distribution. It plots the quantiles of the dataset. Against this is the quantiles of the desired distribution. If the data follows the chosen distribution, the points in the Q-Q plot will approximately lie on the line y = x.

1.3 How to use them together

Histograms and Q-Q plots can tell us a lot about our data. The shape of the histogram can show the type of distribution our data follows. These are normal, skewed, uniform, bimodal, etc. If our data is normally distributed, the histogram should look symmetrical.

Kurtosis and skewness are two statistics that add detail to the shape of the distribution. Skewness measures the asymmetry of the probability distribution of a real-valued random variable about its mean. Positive skewness indicates a distribution with an asymmetric tail extending towards more positive values, while negative skewness indicates a distribution with an asymmetric tail extending towards more negative values.

Kurtosis measures the "tailedness" of the probability distribution. High kurtosis can indicate outliers because data with high kurtosis tend to have a distinct peak near the mean, decline rather rapidly, and have heavy tails.

A Q-Q plot can confirm if our data follows a certain distribution (ie. gaussian). A gaussian distribution is a common assumption in many statistical tests and techniques. If the points in a Q-Q plot lie on the y=x line, it indicates that our data follows the assumed distribution.

Here is a small Python code snippet that illustrates how to create a histogram and a Q-Q plot for a variable:

import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np

# Assuming 'df' is a pandas DataFrame and 'variable' is the column in df you're interested in
variable = df['column_name']

# Creating a histogram
plt.hist(variable, bins=30, edgecolor='black')
plt.title('Histogram of {}'.format('column_name'))
plt.xlabel('Value'); plt.ylabel('Frequency')
plt.show()

# Creating a Q-Q plot
stats.probplot(variable, dist="norm", plot=plt)
plt.title('Q-Q Plot of {}'.format('column_name'))
plt.show()

Histogram & QQ Plots together

2 - Grouped Boxplots

If you want a quick refresher on boxplots & IQR, go here.

2.1 Intro to Grouped Boxplots

A grouped boxplot is also known as a side-by-side boxplot or a multi boxplot. It extends the concept of a simple boxplot by dividing the dataset into subgroups. It then creates a boxplot for each one of these. This allows for comparisons between groups in a visual and intuitive manner.

2.2 Grouped Boxplot vs Simple Boxplot

There is a primary difference between a grouped boxplot and a simple boxplot. It’s the level of detail and comparison they allow. A simple boxplot can give you an understanding of the spread and center of a single group of data. It can also understand potential outliers of a single group of data. A grouped boxplot extends this analysis to groups. This makes it an excellent tool for comparative studies. Here is an example. Comparing the distributions of a variable across different categories or time periods.

Boxplot

Grouped Boxplot

2.3 What it’s useful for

From a grouped boxplot, we can infer not only the characteristics of individual groups but also the differences between these groups. We can compare their centers (medians), spreads (interquartile ranges), and the presence and location of potential outliers. Grouped boxplots can also highlight if the data within groups follow the same distribution or different distributions.

Here is a simple Python code snippet illustrating how to create a grouped boxplot using the seaborn library:

import seaborn as sns

# Assuming 'df' is your DataFrame and 'group' and 'variable' are the columns you are interested in.
sns.boxplot(x='group', y='variable', data=df)
plt.title('Grouped Boxplot of Variable by Group')
plt.show()

In this plot, the 'group' column specifies the categories to be compared, and the 'variable' column is the numeric variable of interest. This code will create a separate box for each unique value in the 'group' column. You can analyze these boxes for differences in median, IQR, and the presence of outliers.

3 - Violin Plot

3.1 What is a Violin Plot?

A Violin plot is an innovative combination of two other types of diagrams:

• The box plot

• The Kernel Density Plot

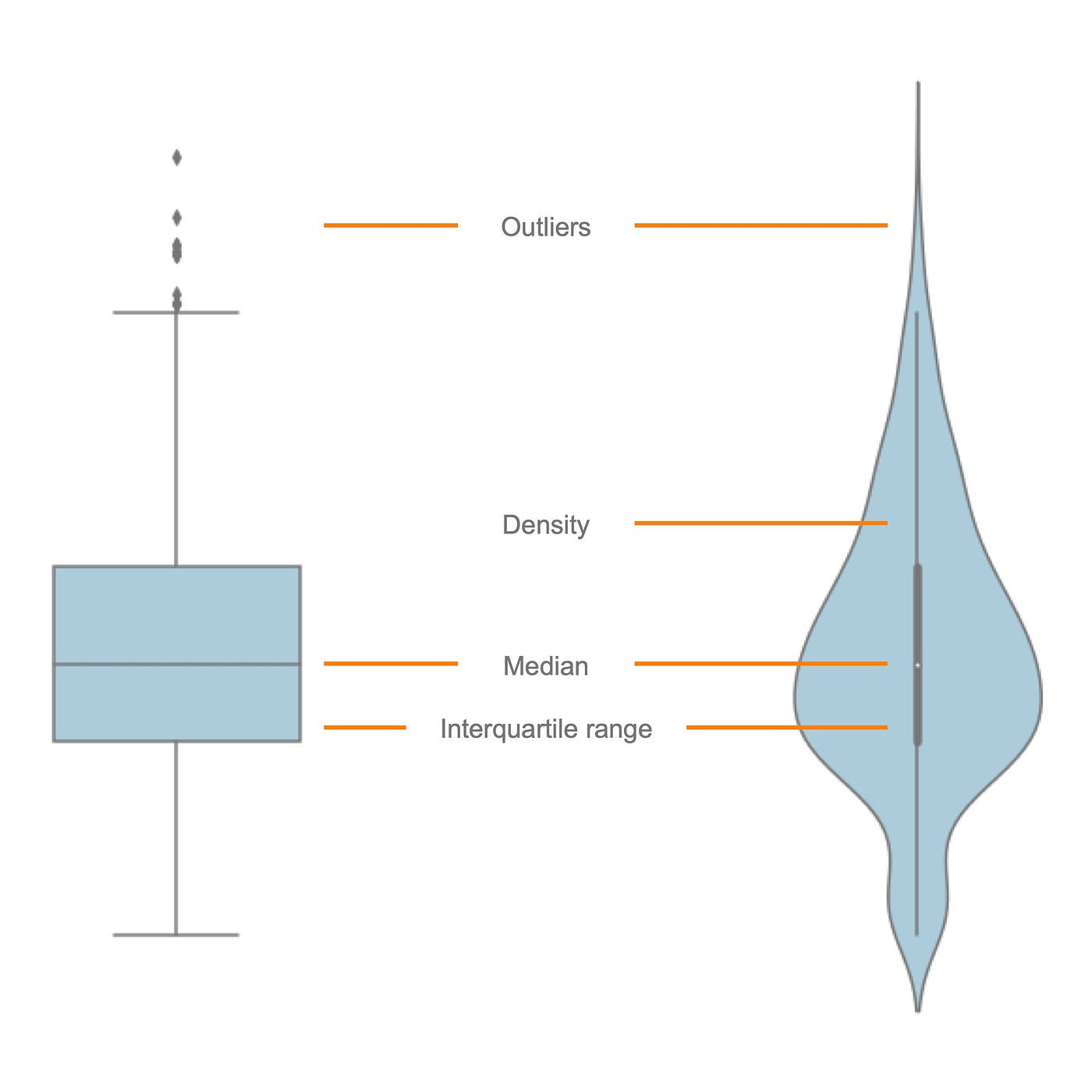
This plot provides a high level of detail about the distribution of data. It features a mirrored and vertical density plot on each side. This is a smoothed version of a histogram, with a boxplot displayed on top of it. This combination allows for a more nuanced understanding of the data distribution. It shows the probability density of the data at different values.

3.2 Analyzing Distribution Shapes

The 'violin' part of a violin plot, the kernel density estimation plot, reveals the density of values at different points in the data, showing where values are concentrated. This makes it excellent for analyzing the shape of the distribution. If the violin is symmetrical around its center, the distribution is likely to be normal. If it is skewed to one side, the data is likely skewed in that direction. If there are more than one peak, the data might be multimodal.

Violin Plot

3.3 Spotting Outliers

While violin plots do not explicitly show outliers like box plots, the kernel density plot can suggest their presence. Sparse areas or 'bumps' at the tails of the violin plot may show potential outliers. When combined with a boxplot, which directly marks outliers, the violin plot becomes a powerful tool for outlier detection.

Here's an example of how to create a violin plot with seaborn:

import seaborn as sns

# Assuming 'df' is your DataFrame and 'variable' is the column you are interested in.
sns.violinplot(x=df['variable'])
plt.title('Violin Plot of Variable')
plt.show()

In this plot, 'variable' is the column whose distribution you want to study. The output will be a violin plot. This plot represents the distribution's density and spread.

Outlier Detection

4 - Scatter Plots

4.1 Bivariate Relationships

In statistics, a bivariate relationship refers to the correlation between two different variables. Studying such relationships can be crucial for understanding the complex interplay between different factors in a dataset. For example, a bivariate analysis could examine the relationship between the height and weight of individuals, test scores and hours of study, or age and income level.

4.2 Scatter Plots

A scatter plot is a useful graphical tool. It’s great for visualizing the relationship between two numerical variables. It consists of a series of dots in a two-dimensional space. Each dot represents an observation. The position of each dot is on the horizontal (x-axis) and vertical axis (y-axis). They correspond to its values for the two variables we are plotting.

Scatter Plot

4.3 Insights you can gather

Scatter plots can help us identify various aspects of bivariate relationships:

• Direction: A positive relationship is identified by an upward trend in the points, while a negative relationship is marked by a downward trend.

• Form: If the points form a straight line, the relationship is linear. If the points form a curved line, the relationship is nonlinear.

• Strength: The closer the points are to a clear form (line or curve), the stronger the relationship.

• Outliers: Points that stand far away from the overall pattern can be identified as outliers.

Here's an example of how to create a scatter plot with matplotlib:

import matplotlib.pyplot as plt

# Assuming 'df' is your DataFrame and 'variable1' and 'variable2' are the columns you are interested in.
plt.scatter(df['variable1'], df['variable2'])
plt.title('Scatter Plot of variable1 vs variable2')
plt.xlabel('variable1')
plt.ylabel('variable2')
plt.show()

In this plot, 'variable1' is the variable represented on the x-axis. 'variable2' is the variable represented on the y-axis. The resulting scatter plot will give you a visual representation. It shows the relationship between these two variables.

Scatter plots are excellent for observing relationships and spotting outliers. Yet, they do not provide a quantitative measure of the relationship strength. For that, you might consider statistical measures like correlation coefficients.

5 - Line Plots

Not much to say here, it’s like a scatter plot, except you have 1 y value, per x value. Then, we just connect a straight line through all of the points.

Here's how to create a simple line plot using Python's matplotlib library:

import matplotlib.pyplot as plt

# Assuming 'df' is your DataFrame and 'time' and 'variable1' are your columns.
df.sort_values('time', inplace=True)  # Ensure the data is in correct time order.
plt.plot(df['time'], df['variable1'])
plt.title('Trend of variable1 Over Time')
plt.xlabel('Time')
plt.ylabel('variable1')
plt.show()

This will generate a line plot that visualizes how 'variable1' changes over 'time', enabling you to spot any upward or downward trends and any abrupt changes that could indicate outliers or errors in the data.

6 - HeatMaps

6.1 Correlation Matrices

In statistical analysis, a correlation matrix is a table. This table displays the correlation coefficients between several variables. Each cell in the table represents the correlation between two variables. The correlation coefficient ranges from -1 to 1. A value close to 1 indicates a strong positive correlation. A value close to -1 indicates a strong negative correlation, and a value close to 0 implies a weak or no correlation. Use this valuable information. Use this to understand the relationships between different variables in your dataset.

In Python, you can compute the correlation matrix of a pandas DataFrame using the corr() method. Here's an example:

# Assuming 'df' is your DataFrame.
corr_matrix = df.corr()

6.2 Heatmap on a Correlation Matrix

Heat maps are especially effective when used in conjunction with correlation matrices. The color-coded heat map helps to visualize the correlation matrix. This makes it easier to interpret.

Here's how you can create a heat map from a correlation matrix using seaborn. This is a Python data visualization library:

import seaborn as sns

sns.heatmap(corr_matrix, annot=True)
plt.show()

In this code, sns.heatmap() creates the heat map, and annot=True ensures that the correlation values are displayed on the map.

Heatmap on a correlation matrix

6.3 Insights you can gather

By examining the heat map, you can identify highly correlated variables very fast. Here is what it would mean if two variables are highly positively correlated. (Approaching 1). They increase or decrease together indicating a possible cause-and-effect relationship or influence. Here is what it would mean if the correlation is strongly negative. (Approaching -1). When one variable increases, the other decreases, and vice versa.

Yet, it's essential to note that correlation does not imply causation. Two variables may have a strong correlation between two variables. This doesn't always mean that changes in one variable cause changes in the other. Nonetheless, correlation and heat maps can serve as useful starting points. It can used for further investigations into the relationships among variables.

Heat maps of correlation matrices also provide insights that can guide model selection. For instance, in linear regression models. Highly correlated independent variables. This is a situation known as multicollinearity. It can undermine the model's performance. Recognize this early in the data exploration phase. It can help you choose appropriate models or data transformations.