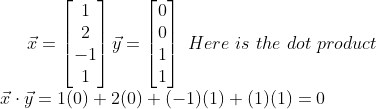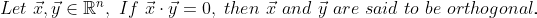Linear Algebra 3: Products, Length, and Orthogonals
Cross/Dot Products, Length (Norm) of a vector, and checking if two vectors are orthogonal (dimensionality reduction)
Note: For this one, we will heavily rely on libraries. If you do not know how to use them, click here. Also, every single linear algebra post will start to build on the previous one. Click here to go to part 1 if you are unfamiliar with it.
Table of Contents:
What should you Pay Attention to?
Dot Products
Length (Norm) of a Vector
Orthogonal
Cross Products
1 - What should you Pay Attention to?
Research Roles: if you are interested in a research heavy role such as a Natural Language Processing researcher, or a Machine Learning Engineer. Then your role will require an extremely heavy usage of linear algebra, so you will want to pay attention to everything in the Linear Algebra series.
A business heavy Data Science Role: In this role, it’s more important to know the business domain knowledge first, and then linear algebra second. In your case, you will want to do a quick gloss over the concepts section, so that you know what the specific calculation does, and then a quick gloss over on the coding section for it too.
Data Analyst: Honestly, as long you know how to use the numpy, or the functions in R, you are basically fine. The expectation for linear algebra are not that heavy for you guys.
2 - Dot Products
Concept
Assuming you remember some stuff from grade 12, then you know in a dot product, all we do is multiply the rows of each of the 2 vectors, and then add them up, and then repeat this for every single row in the vectors. Lastly, we add up all the rows in the end for 1 simple number. Here is the mathematical interpretation:
Example:
By Hand
Let’s say we have the vectors x=[1,2,-1,1], and y=[0,0,1,1]. Here is how you do the calculation by hand:
In R
In order to calculate the dot product of 2 vectors in R, we can use the %*% function.
Hint: It is basically a simple matrix multiplication being done on 2 vectors. We’ll get to matrices soon though.
In Python
In Python, we will first use the numpy library to make an array from our list. This will treat the array as a simple vector. We will then use the .dot() method available from the numpy library to do the calculation. Here is what it looks like:
3 - Length (Norm) of a Vector
Concept
The length of a vector is simply the distance between two points. Generally speaking, when we are looking at the distance, we always assume that we start at the origin (0,0), and we try to calculate the distance all the way to the coordinates given in the vector itself (we assume it ends there). To do this, we simply just use the Pythagorean theorem. Here is the formula for it:
Example
By Hand
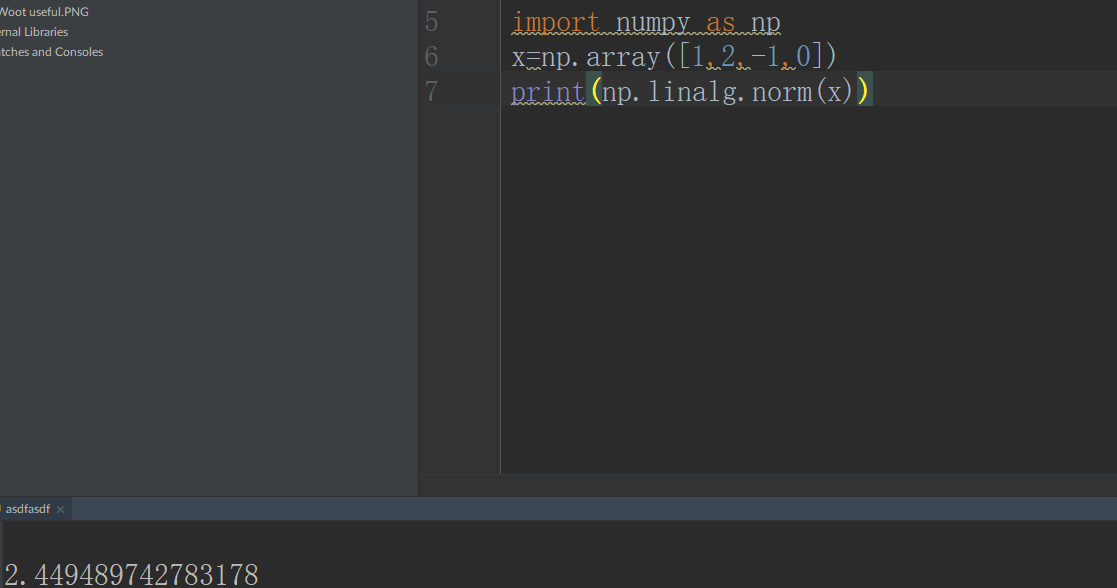
Let x = [1,2,-1,0] Here is the length of this vector:
In R
To calculate the length of a vector, we can just use the norm() function on a vector. Just be sure to specify type='2', or else it will think you are trying to get the norm for a matrix instead of a vector.
In Python
We will rely on the numpy library once more, as it is basically like our bread and butter when dealing with linear algebra in Python. To do this, we will rely on the norm() function, inside the linalg directory inside the numpy library.
4 - Orthogonal
Concept
If the dot product of two vectors is 0, we say that these 2 vectors are orthogonal. ALL vectors that are orthogonal are said to be linearly independent. This is important for us in data science because if we have a set of vectors, we can kick out all the vectors, until we only have orthogonal ones, and we will not lose any information. Here is the mathematical interpretation of it:
Note: Every single vector that is orthogonal is linearly independent. But, every single vector that is linearly independent doesn’t have to be orthogonal. Here is an example of one such pair: {x=[1,1], y=[1,0]}
In the real world, checking for linear independence is a set of thousands of vectors is extremely time consuming. So, in order to deal with this headache, and implement some dimensionality reduction, we instead just check if set of vectors are orthogonal. It isn’t a perfect way to reducing the number of vectors, however it is much faster than manually checking for linear independence.
Example
By Hand
Let’s check if x=[1,0,1,2] and y=[2,3,-4,1]
In R
To check if two vectors are orthogonal, we can just create a simple conditional expression, alongside a calculation of a dot product.
In Python
We can do the exact same thing in Python. Just a simple conditional expression, alongside a calculation of a dot product.
5 - Cross Products
Concept
The cross product just tells us what the orthogonal is to the 2 vectors we are looking it. Let’s say we have 2 vectors: x, y. Then the cross product of these two vectors is a new vector which is orthogonal to them both. Here is the mathematical calculation:
Since we are more focused on the actual DS side of things, I’m not going to go through the effort of putting the proofs for any ling alg calculations here. You can see the proof here if you are interested.
Example:
By Hand
Let’s say we have x=[0,1,0], y=[1,0,0]. Then to find the cross product of x and y. We can do this:
In R
To do this one super easily, we can just load up the pracma library in R. From there, we can use the cross() function, and input our 2 vectors in there.
In Python
To do this easily in Python, we use the numpy library to make two simple vectors. From there, we can use numpy’s cross function in order to run a cross product on our two vectors.